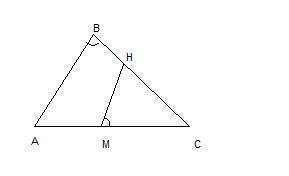
А) Треугольники АВС и СМН подобны по первому признаку подобия: два угла одного треуг-ка соответственно равны двум углам другого. В нашем случае угол С - общий, а углы АВС и СМН равны по условию. Поскольку треугольники подобны, то
б) Поскольку треугольники АВС и СМН подобны, то их сходственные стороны пропорциональны. Сходственными сторонами в данном случае будут стороны СН и АС, МН и АВ, СМ и ВС. Для этих сторон можно записать:
МН : АВ = СМ : ВС. Отсюда следует, что, если МН < СМ, то и АВ < ВС