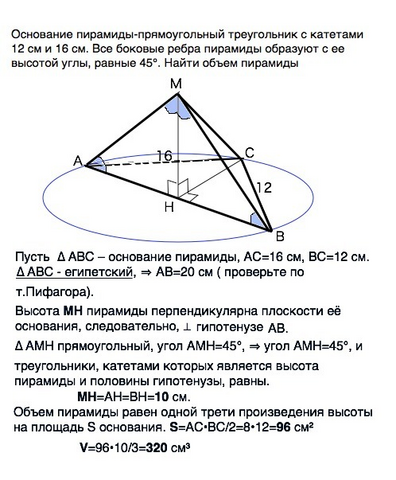
Основание пирамиды-прямоугольный треугольник с катетами 12 см и 16 см. Все боковые ребра пирамиды образуют с ее высотой углы, равные 45°. Найти объем пирамиды.
Решение.
Пусть ∆ АВС – основание пирамиды, АС=16 см, ВС=12 см.
∆ АВС - египетский, ⇒АВ=20 см ( проверьте по т.Пифагора).
Высота МН пирамиды перпендикулярна плоскости её основания, следовательно, перпендикулярна гипотенузе АВ.
∆ АМН прямоугольный, угол АМН=45°, следовательно, угол АМН=45°, и треугольники, катетами которых является высота пирамиды, половины гипотенузы и медиана, равны.
МН=АН=ВН=10 см.
Объем пирамиды равен одной трети произведения высоты на площадь S основания. S=AC•BC/2=8•12=96 см²
V=96•10/3=320 см³