Докажите, что большая боковая сторона описанной прямоугольной трапеции равна удвоенной...

Question

Докажите, что большая боковая сторона описанной прямоугольной трапеции равна удвоенной разности средней линии и радиуса вписанной окружности.
Заранее спасибо;-)

Answer 1

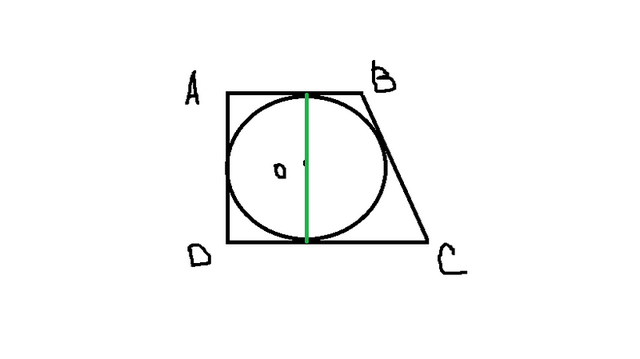
Если в четырехугольник вписана окружность, значит суммы противолежащих сторон равны. На чертеже AB+CD=AD+BC. Тогда BC=AB+CD-AD.
Средняя линия равна (AB+CD)/2=L
AD равен 2 радиусам (на чертеже видно, что зеленая линия - диаметр - равен AD).
Тогда:
BC=2(L-r)

---