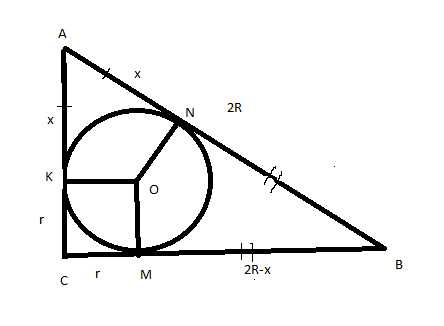Радиусы вписанной и описанной около прямоугольного треугольника окружностей равны...

Question

Радиусы вписанной и описанной около прямоугольного треугольника окружностей равны соответсвенно 3 и 11. найдите площадь треугольника

Answer 1

Радиус описанной окружности прямоугольного треугольника (R):
R=c/2, гипотенуза c=2R=2*11=22
Радиус вписанной окружности в прямоугольный треугольник (r):
r=(a+b-c)/2, а+b=2r+c=2*3+22=28. а=28-b.
Также a²=c²-b²=484-b².
 (28-b)²=484-b².
784-56b+b²=484-b².
b²-28b+150=0.
D=184
b1=(28-2√46)/2=14-√46. а1=14+√46
b2=14+√46. а2=14-√46
 Площадь треугольника S=ab/2=(14-√46)(14+√46)/2=(196-46)/2=75

Answer 2

Диаметр окружности, описанной около прямоугольника треугольника равен гипотенузе.Значит гипотенуза АВ=2R=22.
На рисунке изображена окружность, вписанная в прямоугольный треугольник.
По свойству касательной, проведенной к окружности из одной точки, отрезки касательных равны.
Значит АК=AN=х, BN=22-x=BM
Катет АВ=х+r=x+3
катет ВС=r+22-x=3+22-x=25-x
По теореме Пифагора АВ²+ВС²=АС²
(х+3)²+(25-х)²=22²
или
х²+6х+9+625-50х+х²=484,
2х²-44х+150=0,
х²-22х+75=0,
D=b²-4ac=(-22)²-4·75=484-300=184=(2√46)²

х₁=(22-2√46)/2  или х₂=(22+2√46)/2

х₁=11-√46  или х₂=11+√46
Тогда  при  х₁=11-√46  катет АВ=3+11-√46=14-√46,
а катет ВС=3+22-(11-√46)=14+√46
или наоборот, при х₂=11+√46  кате АВ=3+11+√46=14+√46, а катет ВС=3+22-(11+√46)=14-√46.
Площадь прямоугольного треугольника равна половине произведения катетов:
S=1/2 (11-√46)(11+√46)=(формула a²-b²)=1/2(11²-46)=(121-46)/2=75/5

---