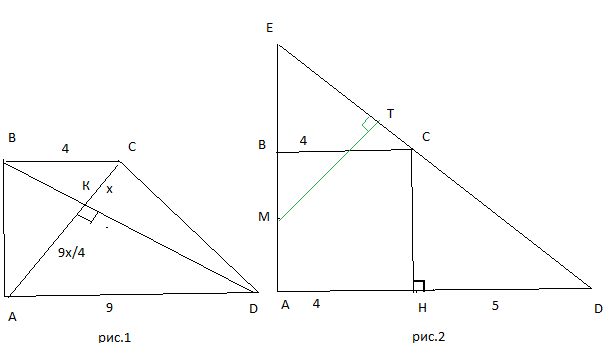
См. рис.1
Треугольники ВКС и AKD подобны по двум углам:
угол СВК равен углу BDA- внутренние накрест лежащие при параллельных прямых ВС и AВ и секущей BD.
угол ВСК равен углу CAD-внутренние накрест лежащие при параллельных прямых ВС и AВ и секущей АС.
Из подобия треугольников СК:АК=ВС:AD=4:9.
Пусть СК=х, тогда АК=9х/4
По теореме Пифагора из прямоугольного треугольника ВКС: ВК²=ВС²-КС²=16-х²
Из прямоугольного треугольника АВК: АВ²=ВК²+АК²=16-х²+81х²/16=16+65х²/16.
Из прямоугольного треугольника АВС: АС²=АВ²+ВС²
(х+9х/4)²=16+65х²/16+16,
(13х/4)²-65х²/16=32,
104х²/16=32,
52х²=256
х²=256/52
Тогда АВ²=16+(65·256)/(52·16)=36
АВ=6
По теореме Пифагора из треугольника СНD (см. рисунок 2):
CD²=5²+6²=√61
Продолжим стороны трапеции до пересечения в точке Е
Треугольники ВСЕ и СНД подобны по двум углам.
ВЕ:СН=4:5 ⇒ВЕ=4,8
Середина АВ-точка М. АМ=МВ=3. ВМ=4,8+3=7,8
В треугольнике СНD sin HСВ=5/√61
sin ВЕС=sin HCB=5/√61
Из треугольника ВМТ: МТ=ВМ·sin ВЕС=7,8·5√61=39/√61