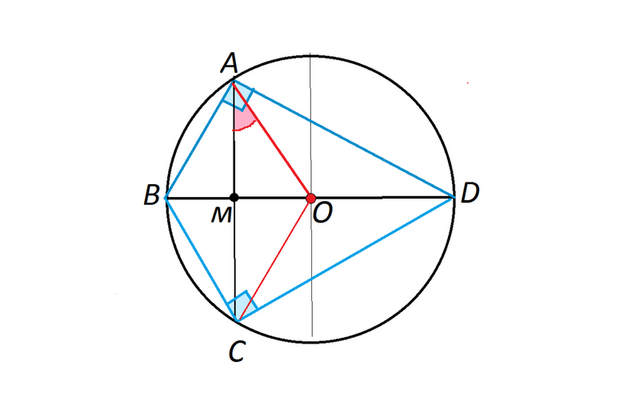
Отрезок BD - диаметр окружности с центром О. Хорда AC делит
пополам радиус OB и перпендикулярна к нему. Найдите углы
четырёхугольника ABCD и градусные меры дуг AB BC CD и AD.
---------
Соединим центр окружности с вершиной А.
Отрезок ОА -
радиус, МО равен его половине.
Синус угла МАО равен МО
:АО=
1/2.
Это синус 30°
∠ МАО=30°, ⇒ угол
АОВ=60°.
ВО=АО=радиус окружности.⇒ △ АОВ равнобедренный.
Сумма углов треугольника 180 градусов.
∠ ОВА=∠ОАВ=(180°-60°):2)=60° ⇒
△ АОВ- равносторонний.
Углы ВАD и ВСD опираются на диаметр ⇒ они прямые
=90°.
⊿ ВСD и ⊿ВАD -прямоугольные, и
∠СDВ=∠АDВ=180°-(90°-60°)
=30°
⊿ ВСD=⊿ВАD.
∠ D=2
·∠АDВ=2
·30°=60°
Сумма углов четырехугольника 360°
∠АВС=360°- 2
·90°- 60°=
120°
Градусная мера дуги равна центральному углу, который на нее
опирается.
На дугу АВ опирается центральный угол АОВ=60°⇒ ее градусная мера 60°
На СВ опирается центральный угол СОВ=60°⇒ ее градусная мера 60°
В треугольнике САD ∠САD=∠DАС=60°
Вписанный угол равен половине градусной меры дуги, на которую
опирается.
На дугу CD опирается вписанный угол САD=60°⇒ она равна 2
·60°=120°
На дугу АD опирается вписанный угол АСD=60°⇒ она равна 2
·60°=120°
Ответ
:
∠А=С=90°
∠В=120°
∠Д=60°
градусные меры дуг
AB=60°
BC=60°
CD=120°
AD=120°.