Площа прямокутної трапеції 126 см² а її основи 11 і 17 см. знайти більшу бічну сторону

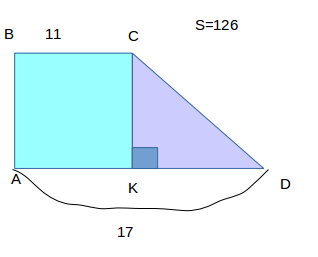
Дано: ABCD - Прямокутна трапеція, ВС = 11 см, АD = 17 см, S = 216 см².
Знайти: СD.

Розв'язання:
1.З загальної площі трапеції знайдемо висоту

$S= \frac{a+b}{2} *h$ , де а - більша основа AD, b - менша основа ВС, h - висота CK

$CK= \frac{2*S}{AD+BC} = \frac{216*2}{11+17}=9$

2.Знайдемо KD

АК = 11 см, тому АBCK - квадрат, а у квадрата всі сторони рівні, звідси

KD = AD - AK = 17-11 = 6 см

3. З прямокутного трикутника CDK(∠ CKD=90)

За теоремою Піфагора

$CD^2=CK^2+KD^2 \\ \\ CD= \sqrt{CK^2+KD^2} = \sqrt{9^2+6^2} = \sqrt{117} =3 \sqrt{13}$ см

Отже, CD = 3√13 см

Відповідь: 3√13 см.