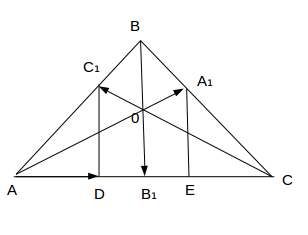
Позначимо D і E проекції точок C₁ і D₁ на пряму AC. Тоді з рівності
B₁B = -BB₁=AA₁+CC₁ для проекцій на пряму АС одержимо рівність:
AE +CD =0. Оскільки AE = AD + DE і CD = CE + DE, знаходимо що AD + CE =0, тобто AD = EC. Звідси, |AD| = |EC|.
З прямокутних трикутників AC₁D і ACC₁, маємо: |AD| = |AC| *cos²∠ A;
|EC| = |AC| *cos²∠ C. Оскільки |AD| = |EC|,то cos²∠ A=cos²∠ C. Аналогічно доводиться, що cos²∠ A = cos²∠ B.
Звідси випливає що ∠ A=∠ B=∠ C, тобто трикутник АВС - правильний.
Що й треба було довести.