Диагонали равнобокой трапеции взаимно перпендикулярны. Найти площадь трапеции, если...

Question

Диагонали равнобокой трапеции взаимно перпендикулярны. Найти площадь трапеции, если основания её равны 6см и 10см.

Comments

перезагрузи страницу если не видно

Answer 1

  Воспользуемся известным соотношением , если диагонали равнобедренной трапеций перпендикулярны 
 

Answer 2

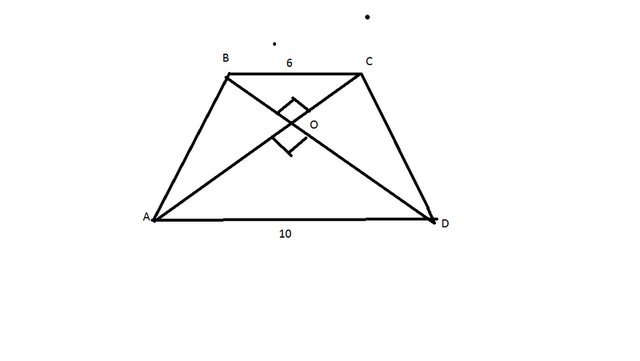
Тк равнобокая трапеция то  из симетрии.
Треугольники  BOC и  AOD равнобедренные и  прямоугольные.
Откуда  по  теореме пифагора: AO=10/√2   OC=6/√2
Откуда диагонали  трапеции  равны:D1=D2=16/√2
А  площадь  любого  4 угольника вычисляется  как  полупроизведение  диагоналей на  синус  угла между ними,в   данном  случае sin90=1
S=1/2*(16/√2)^2=256/4=64
Ответ:64
В  принципе  для решения  достаточно  1  средней  линии

---

Comments

равнобедренный прямоугольный треугольник x^2+x^2=36 2x^2=36

---

а как по теореме пифагора АО и ОС находится?

---

x=6/sqrt(2) так же другое основание