** основании AC равнобедренного треугольника ABC как ** диаметре построена окружность,...

Question

На основании AC равнобедренного треугольника ABC как на диаметре построена окружность, которая пересекает сторону AB в точке D, BC - в точке E. Определите сторону AB, если AD=30 см, а хорда DE равна 14 см.

Answer 1

Так как треугольник равнобедренный, то центр окружности О лежит посредине стороны АС, тогда ВО- высота, медиана и биссектриса треугольника АВС.
Точка К - точка пересечения DE и ВО.
АDВО - прямоугольная трапеция, у которой нижнее основание АО=r (r-радиус окружности), верхнее основание DК=14/2=7, меньшая диагональ ОD=r, боковая сторона АD=30 и высота КО=h.  В этой трапеции опустим высоту DН=KO, тогда
АH=АO-НО=АO-DК или  AH=r-7
DH²=OD²-DК²  или   h²=r²-7²=r²-49
AH²=AD²-DH² или АН²=30²-h²=900-h²=900-r²+49=949-r²
Приравниваем АН и получаем
949-r²=(r-7)²
2r²-14r-900=0
r²-7r-450=0
D=49+1800=1849=43²
r=(7+43)/2=25 см
Так как треугольники АВО и DBK подобны  по 2 углам (углы АОВ=DKB=90, угол АВО -общий), то коэффициент подобия к=DK/AO=7/25
Тогда DВ/AВ=7/25, а DВ=АВ-АD=АВ-30
25(АВ-30)=7АВ
18АВ=750
АВ=750/18=125/3

Comments

Еще один вариант решения.
Соединив D и С, получим прямоугольный треугольник АDС, в котором высота DН делит диаметр АС ( гипотенузу) по свойству высоты равнобедренной трапеции на два отрезка:
АН=r-7, и HC=r+7
Катет АD прямоугольного треугольника АDС - среднее пропроциональное между отрезком АН и гипотенузой АС
АD² =АН*АС
900=2r² -14r
r² -7r-450=0 Решив квадратное уравнение, получим
r=25
Из подобия АВС и DВЕ найдем DВ=35/3
И АВ=125/3 или 41 и 2/3

Answer 2

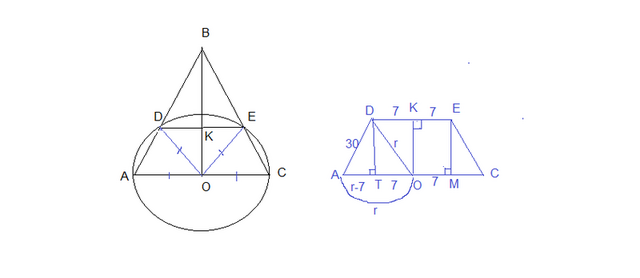
См. рисунок.
Треугольник АВС- равнобедренный. Углы при основании равны, поэтому угол А равен углу С. Угол А вписанный и опирается на дугу DEC,
Угол С вписанный и опирается на дугу ADE.
Дуга DE- общая, значит дуга AD равна дуге ЕС.
Поэтому  DE || AC.
Проведем радиусы ОD и ОЕ.
АО=ОС=OD=ОЕ=к=r,  r - радиус окружности.
Треугольники ADO и OEC
ВО- высота равнобедренного треугольника является и его медианой, АО=ОС,
Так как DE|| AC, то ВО делит DE пополам и DK=KE=7
Проведем высоту  DT. TO=7, AT=r-7
Из прямоугольного треугольника DTO по теореме Пифагора   DT²=DO²-TO²=r²-7²
Из прямоугольного треугольника ADT по теореме Пифагора   DT²=AD²-АT²=30²-(r-7)²
Приравняем правые части равенств, получим: r²-7²=30²-(r-7)²,
Решаем квадратное уравнение:
r²-49=900-(r²-14r+49),
r²-7r-450=0
D=49+1800=1849=43²
r=(7+43)/2=25, r=(7-43)/2<0<br> r=25
Треугольник DBK подобен треугольнику ABO
Пусть BD=x.
BD: AB=DK:AO
x:(x+30)=7:25
применяем основное свойство пропорции: произведение крайних членов х и 25 равно произведению средних (х+30) и 7
25х=7х+210
18х=210.
х=35/3

АВ=30+35/3=(90+35)/3=125/3

---