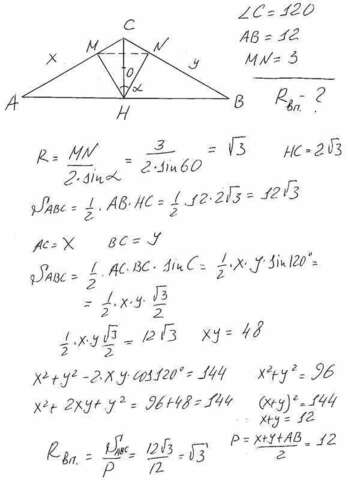
Обозначим треугольник АВС(смотри рисунок). Угол "альфа"=60, поскольку в четырёхугольнике НМСN сумма остальных углов равна 90+120+90=300. По теореме синусов находим радиус окружности описанной вокруг треугольника НMN. Поскольку точки M и N, принадлежащие прямоугольным треугольникам СМН и СNН лежат на одной окружности , то окружность описанная вокруг НМN будет также описанной окружностью вокруг треугольников СМН и СNН. У прямоугольных треугольников центр этой окружности лежит на середине гипотенузы, отсюда находим высоту НС. Затем площадь треугольника АВС. Потом, по теореме косинусов-найдём сумму квадратов неизвестных сторон. Добавим к ней произведение Х*У и найдём полупериметр. А дальше по известной формуле Радиус вписанной окружности треугольника АВС равен - 12 корней из3/((4 корня из3)+6).