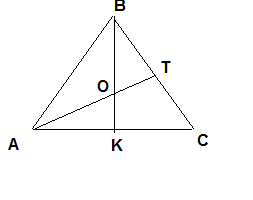
АВС- правильный треугольник. ВК, АТ- медианы. ВК=АТ= 9 см.
АК=КС.
В равнобедренном треугольнике медиана является высотой и биссектрисой.
В равностороннем тем более. Значит O- центр описанной и центр вписанной окружностей.
Медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
ВО:ОК=2:1, значит ВО=6 см, ОК=3 см.
AO:OT= 2:1, AO=6 см, ОТ= 3 см.
Так как ВК- высота, то угол ВКА- прямой.
Из прямоугольного треугольника АОК по теореме Пифагора АК²=АО²-ОК²=6²-3²=36-9=27
АК=3√3
АС=2АК=6√3 см
АВ=ВС=АС=6√3 см