Любые три точки, не лежащие на одной прямой, можно соединить в треугольник.
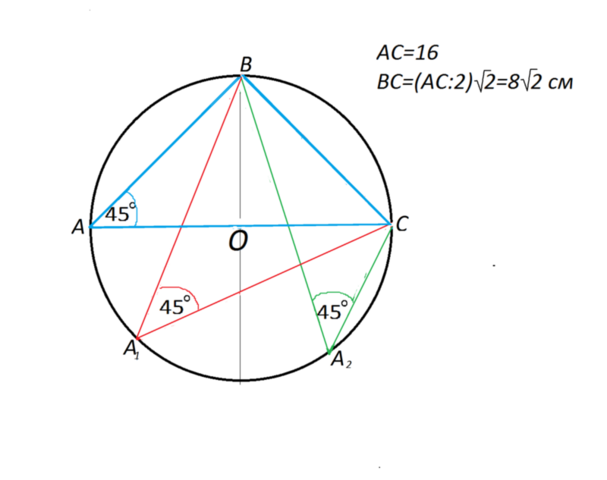
Соединив А, В, С - получим треугольник, вписанный в данную окружность. Хорда ВС - сторона этого треугольника.
Сторону ВС можно вычислить по теореме синусов.
ВС:sin (45)=2R
ВС=2R*sin (45°)
ВС=16*(√2/2)=8√2
Где бы ни располагалась точка А, угол САВ, как вписанный и равный 45°, будет равен половине центрального угла, а хорда, стягивающая дугу этого угла, будет одинаковой длины.
Следовательно, треугольник АВС может быть как разносторонним, так и равнобедренным, угол ВАС - опираться на диаметр АС, который равен 16. d=a√2=16
ВС=a=8√2