1) при к=1 х₁= -π/3+π/2=π/6
при к=2 х₁= π/3+π=4π/3
при к=3 х₁= -π/3+3π/2=7π/6
при к=4 х₁=π/3 + 2π
получим две серии ответов : π/6 + πn и π/3 + πm, n,m∈Z
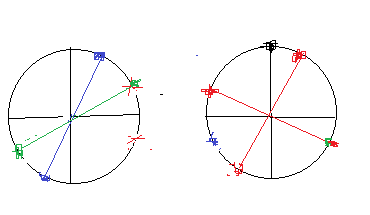
Первая изображена на рисунке зеленым цветом, вторая синим
запишем корни х₂ виде х₂= π/6+2πk и х₂=-π/6+2πk, k∈Z
обе серии изображены красным цветом. На рисунке видно, что пересечением будет π/6+2πk, k∈Z
2) при к=1 х₁=-π/2+π/3=-π/6
при к=2 х₁=π/2+2π/3=7π/6
при к=3 х₁=-π/2+π=π/2
при к=4 х₁=π/2+4π/3=11π/6=5π/6+π=-π/6+2π
при к=5 х₁=-π/2+5π/3=7π/6
при k=6 x₁=π/2++2π
Получили три серии ответов
-π/6+2πn, 7π/6 +2πm, π/2+2πr, n,m,r∈Z
первая изображена зеленым цветом на рис 2, вторая синим, третья черным
при к=1 х₂=5π/6+π/2=4π/3
при к=2 х₂=5π/6+π=-π/6+2π
при к=3 х₂=5π/6+3π/2=14π/6 =π/3+2π
при к=4 х₂=5π/6+2π
эти четыре серии ответов отличаются друг от друга на π/2 и расположены на рисунке 2 красным цветом.
Пересечение х=-π/6+2πk,k∈z