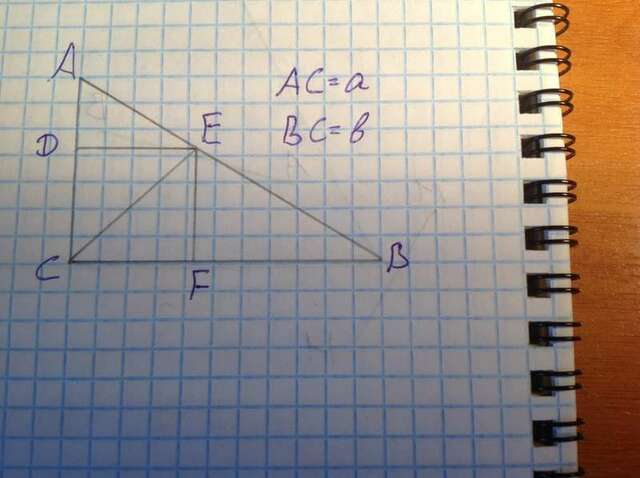Пусть в прямоугольный треугольник ABC вписан квадрат CDEF (см. рисунок). Здесь AC=a, BC=b.
Заметим, что диагональ CE квадрата является также биссектрисой исходного треугольника. Пусть CE=d, тогда CD=d√2/2 - сторона квадрата меньше диагонали в √2 раз. Периметр квадрата равен (d√2/2)*4=2√2d, а площадь равна (d√2/2)²=d²/2. Таким образом, чтобы найти периметр и площадь квадрата, достаточно выразить биссектрису прямого угла d через a и b.
Площадь прямоугольного треугольника равна половине произведения катетов, в нашем случае S=ab/2. Теперь воспользуемся другой формулой площади - S=1/2*a*b*sin(C), где a,b - соседние стороны треугольника, а sin(C) - угол между ними. Тогда S(ACE)=1/2*AC*CE*sin(45), S(BCE)=1/2*CE*BC*sin(45) (углы ACE и BCE равны 45 градусам). Так как S(ACE)+S(BCE)=S(ABC), мы можем записать уравнение с одним неизвестным CE:
1/2*AC*CE*sin(45)+1/2*CE*BC*sin(45)=ab/2
AC*CE*sin(45)+CE*BC*sin(45)=ab
CE(AC+BC)=ab/sin(45)
CE=ab/(a+b)sin(45)
Таким образом, d=ab/(a+b)sin(45). Получаем, что периметр квадрата равен 2√2d=2√2ab/(a+b)sin(45)=4ab/(a+b), а площадь равна d²/2=(ab/(a+b)sin(45))²*1/2=a²b²/(a+b)².