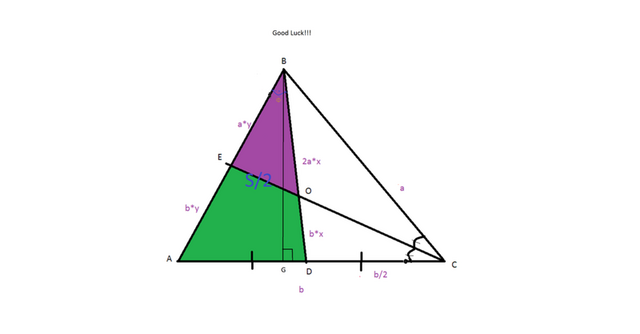
Высота BG общая для треугольников ABC и ABD,то их площади относятся как основы (AC=2AD) . Откуда SABD=S/2
Далее ,по теореме бессектрисы , на рисунке указаны доли отношений. (x,y). Треугольники ABD и EBO имеют общий угол при вершине B (Ф)
Пользуясь этим получим: Если S1-площадь 4 угольника:
SABD/SEBO=0,5*S/(0,5S-S1)=1/2*(a+b)y*(2a+b)*x*sinФ/1/2*ay*2ax*sinФ
=(a+b)(2a+b)/2a^2
S/(S-2s1)=(a+b)(2a+b)/2a^2
S*(2a^2)=(S-2s1)*(a+b)(2a+b)
S*(2a^2-(a+b)(2a+b))=-2s1*(a+b)(2a+b)
S1=S* ( ((a+b)(2a+b)-2a^2)/(2(a+b)(2a+b))
Для того что бы записать формулу в компактном виде примем что b/a=n
S1=0,5*S*((1+n)(2+n)-2)/(1+n)(2+n)=S*n*(n+3)/2(n+1)(n+2)
Ответ: S1=S*n(n+3)/2(n+1)(n+2) где n=b/a