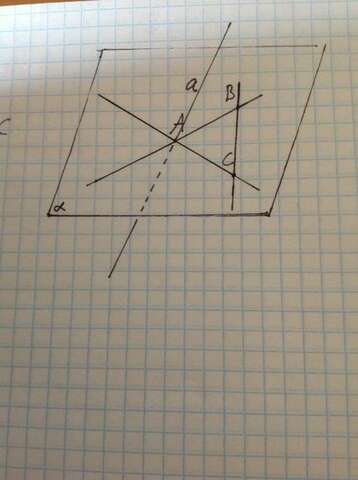
Обозначим за α плоскость, в которой лежат прямые AB и AC (известно, что через две пересекающиеся прямые проходит ровно одна плоскость). По условию, прямая a не лежит в α, но имеет с ней общую точку A. Значит, прямая пересекается с плоскостью и точка A - единственная точка плоскости α, которая принадлежит прямой a. Прямая BC лежит в плоскости α целиком, так как 2 её точки - B и C - принадлежат этой плоскости, и не проходит через A. Если бы a и BC пересекались, существовала бы ещё одна точка в плоскости α, которая бы принадлежала прямой a, но это невозможно. таким образом, a и BC не пересекаются.