В четырехугольнике АВСD диагональ АС делит ∠А пополам. Известно, что АВ=3, ВС=√3, CD=2,...

Question

В четырехугольнике АВСD диагональ АС делит ∠А пополам. Известно, что АВ=3, ВС=√3, CD=2, AD=4. Найдите диагонали и углы четырехугольника АВСD.

Answer 1

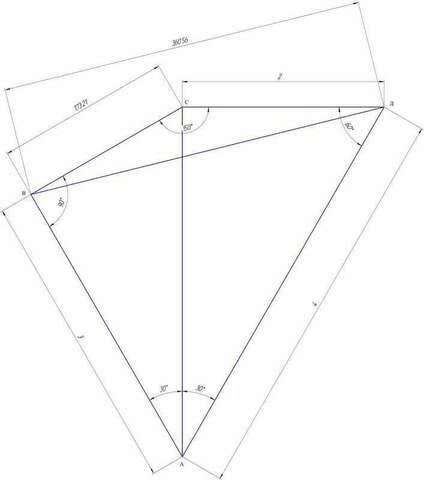
AB^2+AC^2-2AB*AC*cos(a/2)=BC^2
AD^2+AC^2-2AD*AC*cos(a/2)=DC^2
************
-2AB*AC*cos(a/2)=BC^2-(AB^2+AC^2)
-2AD*AC*cos(a/2)=DC^2-(AD^2+AC^2)
************
(BC^2-(AB^2+AC^2))*AD=(DC^2-(AD^2+AC^2))*AB
AC^2*(AB-AD)=(DC^2-AD^2)*AB-(BC^2-AB^2)*AD
AC^2=((DC^2-AD^2)*AB-(BC^2-AB^2)*AD)/ (AB-AD)=
=((2^2-4^2)*3-(3-3^2)*4)/ (3-4)=12
*********************
АВ=3, ВС=√3, CD=2, AD=4, AC = 2√3
***************
cos(a/2)=(BC^2-(AB^2+AC^2))/(-2AB*AC)=(3-(3^2+12))/(-2*3*2*корень(3) ) = корень(3)/2
а = 60 градусов
cos(в)=(АC^2-(AB^2+ВC^2))/(-2AB*ВC) = (12-(3^2+3))/(-2*3*корень(3)) = 0
в = 90 градусов
cos(д)=(АC^2-(АД^2+ДC^2))/(-2AД*ДC) = (12-(4^2+2^2))/(-2*4*2) = 0,5
d = 60 градусов
c=360 -60- 90 - 60 = 150 градусов
ВД = корень(АВ^2+АД^2-2*AB*АД*cos(a))=корень(3^2+4^2-2*3*4*cos(pi/3))= корень(13)

---

Comments

Это же на треугольник больше похож(

---

прикалываемся ?
четырехугольник с углами 60 90 150 60

---

один из углов 150 градусов - близок к 180 - развернутому

---

все, все))

---

Спасибо))

---

Я поняла)

---

рисунок - в масштабе с полным соблюдением пропорций

---

А как эту задачку через осевую симметрию решить?

---

так как стороны неодинаковы, то через осевую симметрию затрудняюсь

---

может попробуете.......