Начну с 10 номера. Он, пожалуй, проще всего. Надеюсь, устроит, если я буду каждую задачу сопровождать подробными объяснениями(я так привык, ничего не поделаешь ;)
Итак, 10 номер.
10
Начну решение задачи с основного факта о касательной к графику.
1)Угловой коэффициент касательной равен значению производной в абсциссе точки касания. Найдём производную нашей функции.
y' = 8x - 5
Угловой коэффициент касательной задан и равен 3. Отсюда по теореме
8x - 5 = 3
8x = 8
x = 1
Таким образом, мы нашли абсциссу точки касания.
2)Теперь воспользуемся фактом, что в точке касания значения обеих функций(касательной и графика самого) равны. Можем приравнять обе формулы, но подставив всюду x = 1.
3x + a = 4x^2 - 5x + 9
Подставляем x =1 и решаем уравнение относительно параметра а:
3 + a = 4 - 5 + 9
3 + a = 8
a = 5
Это ответ.
11
Ну давайте соображать. Очевидно, что одно из чисел должно быть точно целым, иначе никакого числа 16 в произведении не получится.
И тут можно пойти таким путём. Решить задачу перебором. Перебрать все числа от 1 до 16, сравнить суммы. Это вполне законный метод решения таких задач. Так и можно попытаться сделать некоторые вычисления. Скажем, если одно из чисел равно 9, то другое равно 16/9 Их сумма будет явно больше, чем 10.Но этот случай нас явно не устраивает, поскольку если 16 = 2 * 8 = 10, уже меньше этой суммы. Значит, целое число не больше 9. Не может число и 8 быть равным, поскольку тогда 16 = 8 * 2 - сумма этих чисел равна 10, а 16 = 4 * 4 - сумма-то равна 8, не минимальна же она вновь.
Значит, осталось лишь перебрать числа от 3 до 7.
1)Если число равно 3, то другое число равно 16/3. Сумма чуть больше 8. Но этот случай нам не подходит. Сумма может и равна быть 8.
2)Если число равно 4, то это наш случай, 4 + 4 = 8.
Если будем перебирать числа, большие 4, то в сумме получится явно больше 8 - не наш случай. Поэтому, искомое произведение: 16 = 4 * 4
9
Сразу замечу, что морок с одз будет достаточно много. Но начнём с самого начала. У нас произведение, равное 0. Вспоминаем: произведение равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0, а остальные ИМЕЮТ СМЫСЛ. Я эту фразу не зря выделил, он очень важная.
Значит, я перепишу это уравнение в виде совокупности(совокупность - это система условий, в которой может выполняться хотя бы одно из них, либо первое, либо второе, либо же оба. Такой строгости как в системе, в виде того, что обязаны выполняться оба условия, нет).
1 - 1/cos^2 x = 0 ИЛИ 9-x^2 = 0
И
9-x^2 >=0
Легко видеть, что я просто записал в терминах математики вышеназванное утверждение. Теперь решим первую систему, потом второе уравнение(всё вместе это совокупность). А затем объединим полученные решения. Начнём.
Решаем систему.Первое уравнение. Здесь я 1/cos^2 x заменю на 1 + tg^2 x.
1 - (1 + tg^2 x) = 0
1 - 1 - tg^2 x = 0
tg^2 x = 0
Здесь я наложу новое ограничение: cos x не равен 0. Это связано с тем, что косинус - знаменатель, который невидимо, но входит в тангенс(тангенс - это отношение синуса к косинусу).
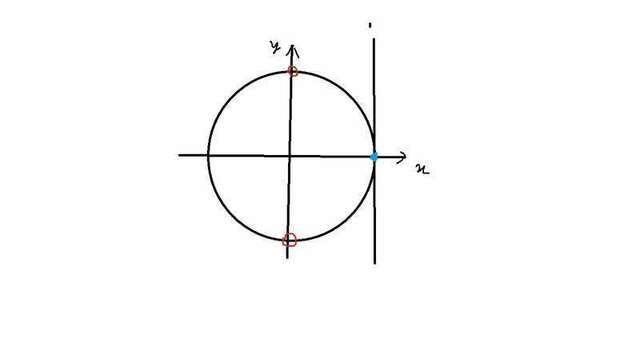
Поэтому, это уравнение я дальше буду решать при помощи тригонометрической окружности. Сейчас нарисую рисунок и приложу сюда.
Видно на окружности у нас есть две точки на окружности, тангенс которых равен 0(голубая точка и ещё одна диаметрально противоположная, которую я почему-то не отметил). Красными значками помечены выколотые точки. косинус которых равен 0. Итак,
x = пиn, n - целое
Решаем второе уравнение системы:
x^2 - 9 <= 0<br>(x-3)(x+3) <= 0<br>[-3;3]
Теперь задача сводится, чтобы найти все корни первого уравнения на отрезке от -3 до 3.
-3 <= пиn <= 3<br> -3/пи <= n <= 3/пи<br>Так как n - целое, то
n = 0 x = 0.
Итак, решением первой системы является число 0.
Теперь осталось решить второе уравнение.
9-x^2 = 0
x^2 = 9
x1 = 3; x2 = -3
Ответ:-3;0;3
8
Исследование функции:
1)D(y) = R
2)Проверим функцию на чётность:
а)D(y) - симметричное множество
б)f(-x) = (-x)^4 - 8(-x)^2 = x^4 - 8x^2 = f(x) - функция чётная. Симметрия относительно оси ординат. Это значит, что достаточно будет построить часть графика при x > 0, а затем просто симметрично достроить остальную часть графика.
3)Определим нули функции.
y = 0 x^4 - 8x^2 = 0
x^2(x^2 - 8) = 0
x = 0 или x1 = корень из 8
x2 = -корень из 8
4)Определим промежутки знакопостоянства функции:
y > 0 x^4 - 8x^2 > 0 на (-беск;-корень из 8) и (корень из 8; +беск)
y < 0 на (-корень из 8; 0) и (0;корень из 8)
5)Определим промежутки возрастания, убывания функции, найдём точки экстремума.
y' = 4x^3 - 16x
y' = 0 4x^3 - 16x = 0
x(4x^2 - 16) = 0
x = 0 или x^2 = 4
x1 = 2; x2 = -2 - стационарные точки
Функция возрастает на [-2;0] и на [2;+беск)
Функция убывает на (-беск;-2] и на [0;2]
x = 0 - точка максимума, y(max) = y(0) = 0
x = -2 - точка минимума,y(min) нужно просчитать
x = 2 - точка минимума, аналогично, просчитываем минимум функции
6)Найдём асимптоты, если они есть.
а)Вертикальных асимптот нет.