Если рассуждать логически то если точка p лежит внутри треугольника. То площадь каждого треугольника в 3 раза меньше площади ABC. Тогда если провести высоты из точки p на стороны и высоты данного треугольника. То высота треугольника на данную сторону в 3 раза больше маленькой высоты на данную сторону. То из теоремы Фалеса следует. Что точка P лежит на отрезке паралельном стороне треугольника и делящем боковые стороны в отношении 2:1 cчитая от вершины. Другими словами она находится в точке пересечения отрезков параллельных основаниям и делящим другие стороны в отношении 2:1 ,считая от противолежащих вершин.
НО в целом медианы тоже cекутся как 2:1. Поэтому из теоремы фалеса точка p1. Точка пересечения медиан. Что в принципе и следовало ожидать :)
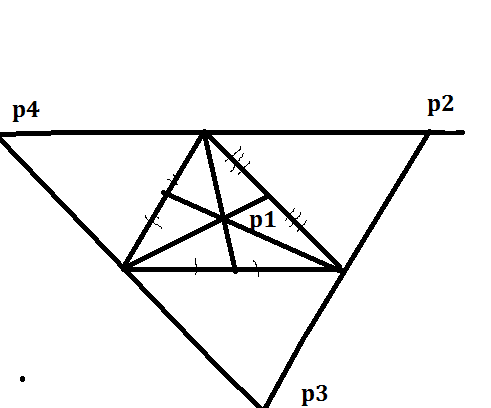
Если точка p лежит вне треугольника. То из рисунка видно что если S площадь нашего треугольника. S1-площади полученных. То
2S1-S1=S S1=S. То есть высоты равны. Точек лежащих вне треугольника всегда 3 лежащих за каждой из сторон треугольника.
Точек лежащих на стыке сторон (на продолжениях высот треугольников нет тк S=S1-2S1<0 ) <br>Из сказанного выше следует что для того чтобы найти эти 3 точки достаточно провести через каждую вершину треугольника прямую параллельную противолежащей стороне. Точки пересечения и дадут 3 данные точки. Таким образом точек всегда 4.
Удачи :)