В треугольнике ABC сторона AB больше стороны BC , ** стороне AB отмечена точка P так,что...

Question

В треугольнике ABC сторона AB больше стороны BC , на стороне AB отмечена точка P так,что PB=BC . Биссектриса BO пересекает описанную возле треугольника ABC окружность в точке K
Доказать,что точки A,K,O,P лежат на одной окружности

Comments

имею рисунок в котором выполняются требования задачи, но точки A,K,O,P не лежат на одной окружности

---

http://smages.com/url/ti5kj6

---

Маленькая ошибка в чертеже : по условию отрезки PB и BC равны :)

---

у вас равными выступают PC и PB

---

неправильно построил (((

---

я ее победил )))

Answer 1

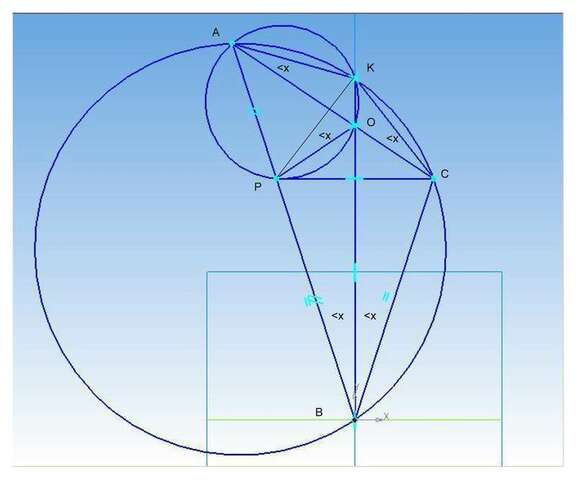
Пусть <КВС = <x - так как ВО - биссектриса<br><КАС = <x - так как опираются на ту же дугу окружности КС что и <КВС = <x<br><КАО = <КАС=<x <br>так как BP = PC и BO - биссектриса, то РСВ - равнобедренный,
значит ВО - серединный перпендикуляр
значит РСК - равнобедренный и РСО - равнобедренный,
значит <КРО = <КСО <br>так как <КСО =<АСК = <x <br>значит <КРО = <x <br>
и наконец
так как в 4-угольнике АКОР
<КАО = <x  и <КРО = <x, значит точки А и Р лежат на некой кривой, из которой отрезок КО виден под одинаковым углом<br>геометрическим местом точек, из которых данный отрезок КО виден под одним и тем же углом является дуга окружности, проходящей через концы отрезка КО
доказано, что точки АКОР лежат на одной окружности

---

Comments

огромное спасибо,выручили))

---

на здоровье
у вас интересные и что немаловажно дорогие задачи )
обращайтесь