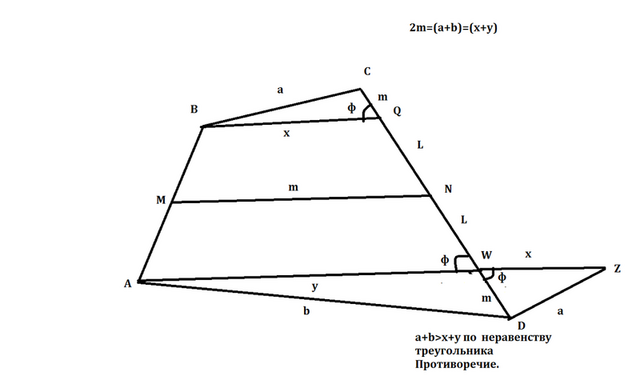
Предположим что:
m=(a+b)/2 ,но a не параллельно b
Сделаем вспомогательные построения:
Проведем сторону BQ=x параллельно m.
И прямую AW=y параллельно m (она же параллельна x)
По теореме Фалеса тк AM=MB,то QN=NW=L
Тк СN=ND,то CQ=WD=m
На продолжении AW отложим отрезок равный x.
Далее из соответственных и вертикальных угол выходит что углы
DWZ и BQC равны. То треугольники BQC и WDZ равны по 2 сторонам и углу между ними. То DZ=BC=a.
То по неравенству треугольника AZD: (a+b)>(x+y)
Тк ABQW-трапеция,а m -ее средняя линия,то
2m=(x+y). По предположению: 2m=(a+b)
То (a+b)=(x+y)
Что противоречит неравенству : (a+b)>(x+y)
То есть мы пришли к противоречию.
Значит BC параллельно AD.
Это решение я назвал (Офигенный кораблик)