1. Используем один из признаков параллелограмма: если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм. В нашем случае:
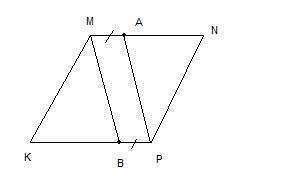
МА=РВ по условию
МА и РВ лежат на параллельных прямых КР и MN, т.к. эти прямые являются противоположными сторонами параллелограмма KMNP (противоположные стороны параллелограмма попарно параллельны).
Значит, АМВР - параллелограмм.
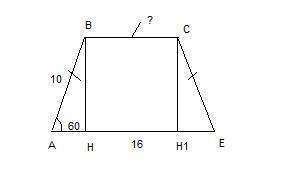
2. Построим высоты трапеции ВН и СН1. Рассмотрим прямоугольный треуг-ик АНВ. Зная косинус угла А, можно найти неизвестный катет АН:
cos 60=AH:AB, отсюда АН=cos 60*AB
AH=1/2*10=5 см
Поскольку трапеция равнобедренная, то АН=ЕН1=5 см.
ВС=НН1. Найдем НН1:
НН1=АЕ-АН-ЕН1=16-5*2=6 см
ВС=6 см