1) область определения функции
1) область определения функции
 -все действительные числа.
-все действительные числа.
2) Производная функции:
Производная постоянной 4 равна нулю.
Производная произведения константы на функцию есть произведение этой константы на производную данной функции.
В силу правила, применим:

Выглядит так:

3) Производная равна нулю
18x=0
x=0
4)
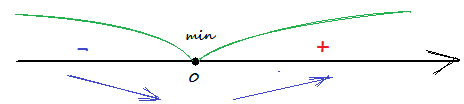
Обозначим на промежутке возрастания и убывания производной.
Проходя через точку минимума, производная функции меняет знак с (-) на (+).
Относительный минимум (0;4).
Итак, функция возрастает на промежутке 
,
убывает -  . В т. х = 0 - функция имеем локальный минимум.
. В т. х = 0 - функция имеем локальный минимум.