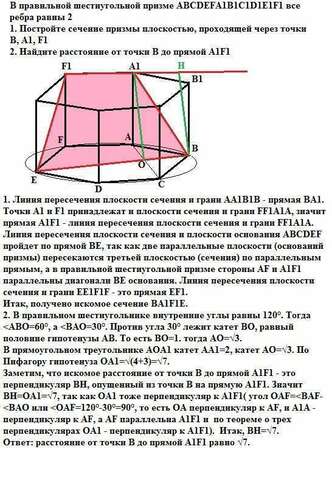
1. Линия пересечения плоскости сечения и грани АА1В1В - прямая ВА1. Точки А1 и F1 принадлежат и плоскости сечения и грани FF1A1A, значит прямая А1F1 - линия пересечения плоскости сечения и грани FF1A1A. Линия пересечения плоскости сечения и плоскости основания ABCDEF пройдет по прямой ВЕ, так как две параллельные плоскости (оснований призмы) пересекаются третьей плоскостью (сечения) по параллельным прямым, а в правильной
шестиугольной призме стороны АF и А1F1 параллельны диагонали ВЕ основания. Линия пересечения плоскости сечения и грани EE1F1F - это прямая EF1.
Итак, получено искомое сечение ВА1F1Е.
2. В правильном шестиугольнике внутренние углы равны 120°. Тогда
В прямоугольном треугольнике АОА1 катет АА1=2, катет АО=√3. По Пифагору гипотенуза ОА1=√(4+3)=√7.
Заметим, что искомое расстояние от точки В до прямой А1F1 - это
перпендикуляр ВН, опущенный из точки В на прямую A1F1. Значит ВН=ОА1=√7, так как ОА1 тоже перпендикуляр к А1F1( угол ОАF=Ответ: расстояние от точки В до прямой А1F1 равно √7.