Исследуйте функцию с помощью производной и постройте график этой функции:y=-x в 4 степени...

Question

Дано ответов: 2

Правильный ответ

$y=-x^4+4x^2-3$
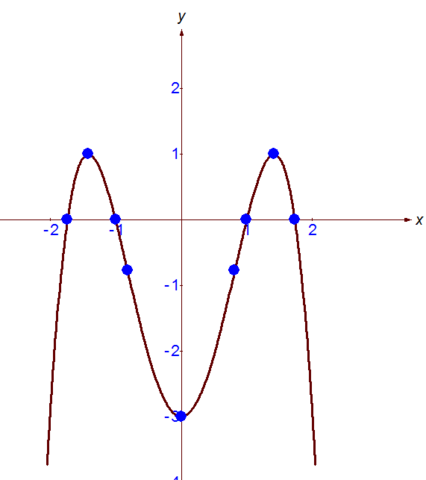
1. Область определения: множество всех действительных чисел
D(y) = R
2. Первая производная
$y'=(-x^4+4x^2-3)'=-(x^4)'+(4x^2)'-(3)'=-4x^3+8x$
3Вторая производная
$y''=(-4x^3+8x)'=-12x^2+8$
4Точки пересечения с осью х:
$x^4-4x^2+3=0 \\ x^2=t,(t \geq 0) \\ t^2-4t+3=0 \\ t_1=1;t_2=3 \\ \left[\begin{array}{ccc}x^2=1\\x^2=3\end{array}\right\to \left[\begin{array}{ccc}x_1_,_2=\pm 1\\x_3_,_4=\pm \sqrt{3} \end{array}\right$

5Точки пересечения с осью у
Пусть х =0
$y=-3$

6 Горизонтальны и наклонные асимтот нет.

7. Критические точки

$-4x^3+8x=0 \\ -4x(x^2-2)=0 \\ x_1=0;x_2_,_3=\pm \sqrt{2}$

8.Точки перегиба
$-12x^2+8=0 \\ x^2= \dfrac{2}{3} \\ x_1_,_2=\pm \dfrac{ \sqrt{6} }{3}$

9. Точки разрыва нет

10. $y(x)-y(-x)=(-x^4+4x^2-3)-(-(-x)^4+4(-x)^2-3)= \\ \\ =-x^4+4x^2+x^4-4x^2=0$
Итак, функция четная, график симметричен относительно оси у

Относительный минимум - $(0;-3)$
Относительный максимум - $(- \sqrt{2} ;1),( \sqrt{2} ;1)$
Множество значений функции: $y \leq 1$

Наибольшее значение: $y =1$

аноним 20 Март, 18

аноним · Answer 1 · 2018-03-20T08:42:01+0000

Y`=-4x³+8x
Найдем экстремумы:
-4x³+8x=0
х=0, х=√2, х=-√2
------------------о------------------------о---------------------о---------------------⇒
+(возвр) -√2 -(убыв) 0 +(возвр) √2 -(убыв)
f(-√2)=1- максимум
f(0)=-3- минимум
f(√2)=1- максимум
Для более точного графика найдем точки пересечения с Ох
-x^4+4x²-3=0⇒x=1, -1, √3, -√3
Вот и все изображай точки и соединяй график будет похож на букву М