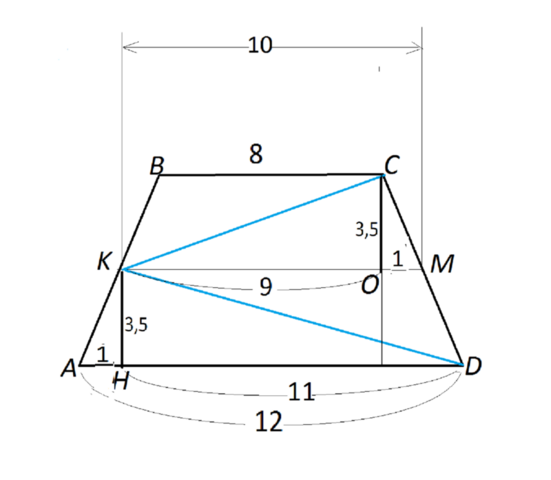
Нарисуем трапецию АВСD.
Проведем ее среднюю линию КМ
КМ=(АD+ВС):2=10
Средняя линия разделила исходную трапецию на две равнобедренные с равными высотами.
Соединим концы стороны СD с серединой К боковой стороны АВ.
Трапеция КВСМ - равнобедренная.
Высота равнобедренной трапеции делит ее большее основание на два отрезка, больший из которых равен полусумме оснований.
КО=(ВС+КМ):2=9
Средняя линия трапеции АВСD разделила ее высоту на два равных отрезка. СО=КН=7:2=3,5
Из прямоугольного треугольника КСО по т.Пифагора найдем СК - один из отрезков, соединяющих концы боковой стороны СD трапеции АВСD с серединой К другой боковой стороны АВ.
СК=√ (СО²+ОК²)=√(12,25+81)=√93,25=0,5√ 373
Второй отрезок DК из треугольника КНD по т.Пифагора:
DК=√(НДD²+КН²)=√(121+12,25)=0,5√533