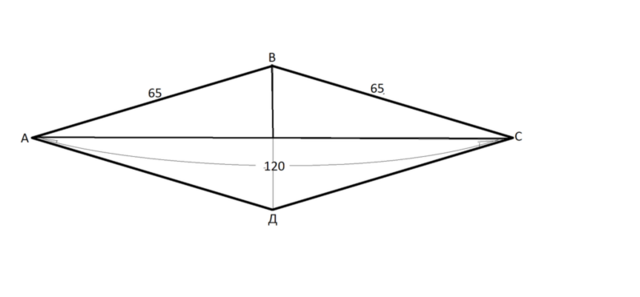
Пусть дан ромб АВСД. АС - диагональ=120, сторона=65.
Стороны ромба равны, и его диагонали пересекаются под прямым углом.
Площадь данного ромба можно найти несколькими способами:.
1) Треугольник АВС - половина ромба. Высота ВН - еще и медиана.
ВН² по т.Пифагора равна АВ²-АН²=65²-60²
ВН=√(4225-3600)=√625=25
Площадь ромба равна 2 площадям треугольника АВС:
S ромба=2*(AС*ВН:2)=3000 (ед. площади)
-
2) По формуле
Герона:
S=√р(p-a)(p-b)(p-c) , где р- полупериметр, и a,b,c- стороны треугольника:
р=(65+65+120):2=125
S=2*√125*(60)*(60)*(5)=√2250000=√225*10000=3000 (ед. площади).
3) Через диагонали.
Площадь ромба равна половине произведения его диагоналей.
Проведем вторую (короткую) диагональ ромба.
Две диагонали разделили ромб на 4 равных прямоугольных треугольника, т.к. в ромбе диагонали пересекаются под прямым углом и, как в любом параллелограмме, точкой пересечения делятся пополам.
В каждом из них гипотенуза равна стороне ромба, а длинный катет равен половине известной диагонали.
Пусть половина неизвестной диагонали равна х.
По т.Пифагора
х²=65²-60²=625
х=25
Вторая диагональ равна 25*2=50
S=50*120:2=3000 ед. площади.
(Можно вычислить площадь одного треугольника и результат умножить на 4)