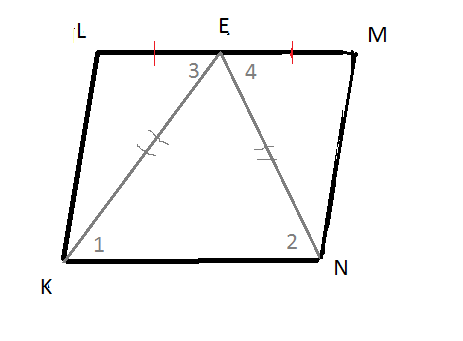
В параллелограмме KLMN точка E - середина LM. Известно, что EK = EN. Докажите, что заданный параллелограмм - прямоугольник.=========================================================================
Решение.
Так как ЕК = EN, то треугольник EKN - равнобедренный, значит ∠1 = ∠2
∠3=∠1 как внутренние накрест лежащие при параллельных прямых LM и KN и секущей КЕ
∠2= ∠4как внутренние накрест лежащие при параллельных прямых LM и KN и секущей ЕN
Получаем, что ∠3= ∠4
Треугольники LEK и EMN по двум сторонам и углу между ними:
ЕК = EN,
LE = EN - так как Е - середина LM
∠3= ∠4
Из равенства треугольников следует, что ∠L= ∠M
Противоположные углы параллелограмма равны между собой
∠L= ∠N
∠K= ∠M
И так как ∠L= ∠M, то все углы параллелограмма равны между собой.
и равны 90°=360°:4
∠L= ∠N= ∠K= ∠M=90°
КLMN - прямоугольник.
: