Вычислить площадь прямоугольного треугольника, если медиана, проведенная к гипотенузе, имеет длину 15 см, а радиус окружности - 4 см
----
Похожую задачу решала на днях.
Ясно, что речь идет о радиусе
вписанной окружности; радиус описанной окружности равен медиане прямоугольного треугольника, а она равна 15 см
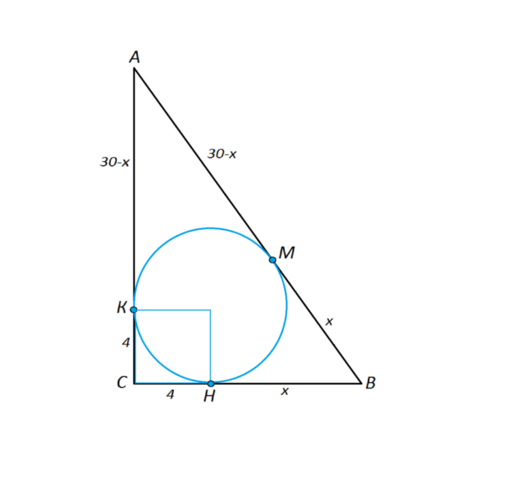
Сделаем рисунок.
Обозначим вершины треугольника А, В, С, а точки касания окружности с его сторонами:
на АС - К,
на СВ-Н,
на АВ-М
Медиана прямоугольного треугоьника равна половине гипотенузы. Следовательно, АВ=15*2=30 см
По свойству касательных из одной точки к окружности
ВН=ВМ,
АМ=АК,
КС=СН=радиусу 4 см
Пусть ВН=х
Тогда ВМ=х, а АМ=30-х
Катет СВ=х+4
Катет АС=АМ+4
АМ=30-х
катет АС=30-х+4=34-х
По теореме Пифагора выразим квадрат гипотеунзы АВ через сумму квадратов катетов:
АВ²=АС²+СВ²
900=(34-х)²+(4+х)²
После возведения в квадрат содержимого скобок и приведения подобных членов получим квадратное уравнение
2х²-60х+272=0
или, сократив на 2,
х²-30х+136=0
D=b²-4ac=-30²-136=356
Дискриминант больше нуля, уравнение имеет два корня:
х₁=(30+2√89):2=15+√89
х₂=(30-2√89):2=15 -√89
Отсюда
АС=34-15-√89=19-√89
ВС=4+15+√89=19+√89
Площадь прямоугольного треугольника равна половине произведения его катетов:
S=(19-√89)(19+√89):2
По формуле сокращенного умножения получим:
S=(361-89):2=136 cм²
Второй корень тоже подходит, просто катеты поменяются размерами, а площадь получится той же величины.