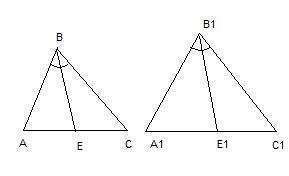
Даны два подобных треугольника АВС и А1В1С1. Соответственные углы у них равны, сходственные стороны - подобны.
Построим биссектрисы ВЕ и В1Е1. Рассмотрим треугольники АВЕ и А1В1Е1. Они также подобны, например, по стороне и двум прилежащим к ней углам:
- т.к. угол В равен углу В1, а ВЕ и В1Е1 - биссектрисы, то угол АВЕ будет равен углу А1В1Е1;
- углы А и А1 равны как соответственные у подобных треугольников АВС и А1В1С1;
- сторона АВ подобна стороне А1В1 по условию, и мы можем написать соотношение этих сторон как
АВ:А1В1=k, где k - коэффициент подобия.
Такое же соотношение сходственных сторон с тем же коэффициентом будет справедливо и для ВЕ и В1Е1 в треугольниках АВЕ и А1В1Е1:
ВЕ:В1Е1=k. Что и требовалось доказать.