В прямоугольном треугольнике ABC катет AC равен 50 а высота CH, опущенная на гипотенузу,...

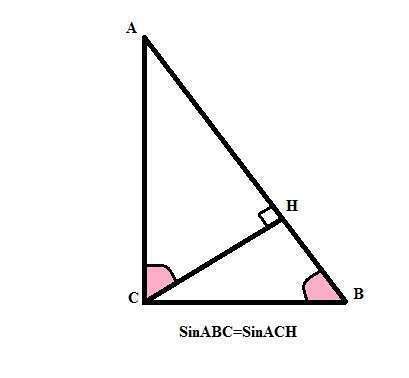
Высота из прямого угла к гипотенузе делит прямоугольный треугольник на два треугольника, подобных данному, отсюда
SinABC=SinACH.
SinACH=√(1-CosACH).
CosACH\=CH/AC или CosACH=8√39/50=4√39/25. Тогда
SinACH=√[(25²-16*39)/25²]=√[(625-624)/25²]=1/25 =0,04.
Или так:
В треугольнике АСН по Пифагору АН=√(АС²-СН²) = √(2500-64*39)=√4=2.
SinABC=SinACH=AH/AC=2/50=1/25=0,04.
Ответ: SinABC=0,04.

В прямоугольном треугольнике ABC катет AC равен 50 а высота CH, опущенная ** гипотенузу,...