Подробное решение.
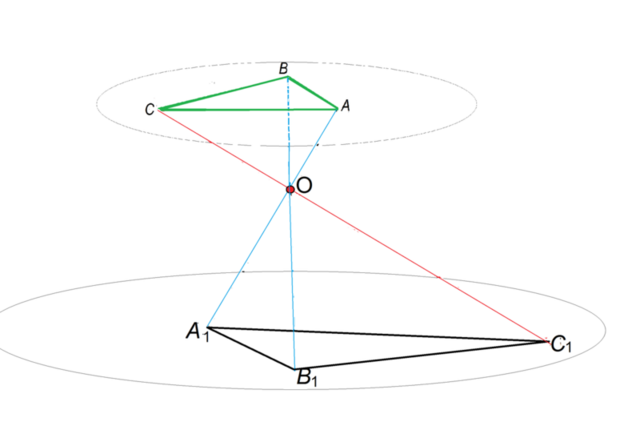
Сделаем рисунок.
Очевидно, что треугольники АВС и А1В1С1 подобны.
Докажем это.
Прямые, которые пересекают плоскости α и β, образуют пересекающиеся прямые.
Через две пересекающиеся прямые можно провести плоскость. притом только одну.
Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
Следовательно, АВ||А₁В₁, ВС||В₁С₁, АС||А₁С₁
В каждой паре треугольников СОВ и С₁ОВ₁, АОВ и А₁ОВ₁, АОС и А₁ОС₁ соответственно углы равны.
Один - как вертикальный, два - как накрестлежащие при пересечении параллельных прямых секущей.
Если углы одного треугольника равны углам другого треугольника, зто такие треугольники подобны.
Отсюда следует подобие треугольников АВС и ,А₁В₁С₁, т.к. их стороны соответственно пропорциональны.
Итак, треугольники подобны.
В подобных треугольниках площади относятся как квадрат коэффициента подобия их линейных размеров.
Площадь треугольника АВС по формуле Герона равна 84 см² ( давать вычисления не буду, их можно сделать самостоятельно. Замечу, что такое отношение сторон треугольника встречается часто, и эту площадь многие знают наизусть.)
Найдем отношение площадей этих подобных треугольников.
S(ABC): S (A1B1C1)=336:84=4
k²=4
k=2
Следовательно, стороны треугольника А₁В₁С₁ в два раза больше сторон треугольника АВС и равны
А₁В₁=26 см
В₁С₁=28 см
А₁С₁=30 см
Для проверки можно вычислить по ф. Герона площадь треугольника А₁В₁С₁ получим 336 см²
—————
[email protected]