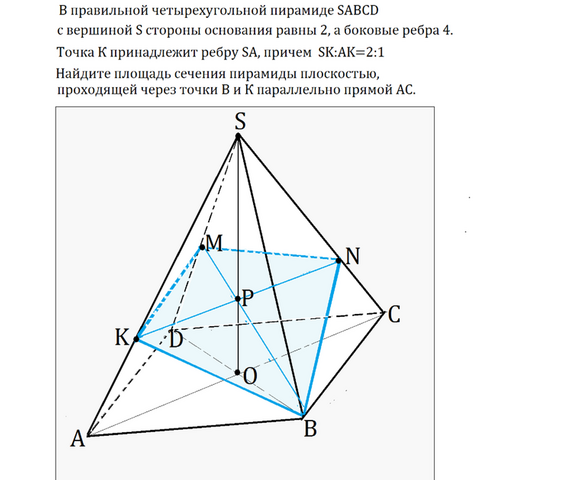
Сделаем рисунок.
Основание данной правильной пирамиды - квадрат ABCD
Из точки К проведем прямую KN параллельно АС.
Прямая параллельна плоскости, когда она параллельна прямой, лежащей в этой плоскости.
Следовательно, АС будет параллельна плоскости, которой принадлежит прямая КN, проведенная параллельно АС, и наоборот, плоскость, в которой лежит КN, параллельна прямой АС.
Рассмотрим треугольник АSС.
В нем КN параллельна АС и отсекает подобный треугольнику АSС треугольник KSC с коэффициентом подобия, следующим из отношения SK:AK
SK - 2 части, AK - 1 часть, AS=3 части.
АS:KS=3:2 ⇒ коэффициент подобия k=3/2
АС:KN=3/2
Диагональ квадрата d=a√2,
сторона квадрата в основании равна 2, ⇒AC=2√2
2√2:KN=3/2
3KN=4√2
KN=(4√2):3
В подобных фигурах все линейные размеры пропорциональны.
SP:PO=SK:AK=2:1
SO- высота пирамиды, а также высота и медиана равнобедренного треугольника DSB, а точка Р, которая делит медиану в отношении 2:1, - точка, в которой пересекаются медианы треугольника.
Прямая ВМ лежит в плоскости сечения, проходит через точку пересечения медиан Р в треугольнике BSD и является его медианой.
АС⊥SO, KN||AC, следовательно,
KN⊥плоскости треугольника DSB и любой прямой, лежащей в этой плоскости.
KN⊥BМ, и эти отрезки - диагонали четырехугольника KMNB, ограничивающего плоскость сечения.
Площадь выпуклого четырехугольника, диагонали которого взаимно перпендикулярны, равна половине произведения этих диагоналей.
Длина диагонали KN уже найдена, она равна (4√2):3.
Длину диагонали МВ, как медианы треугольника SDB, найдем по формуле медианы:
М=0,5√(2а²+2b ² - c ² ), где с - сторона, к которой проведена медиана, а и b - две другие стороны.
М=0,5√(2SB²+2BD² - SD² )
М=0,5√(32+16 - 16 )=0,5√32=2√2
S KMNB=((2√2)*(4√2):3)):2=8/3 = 2 ²|₃ (единиц площади)
-------
[email protected]