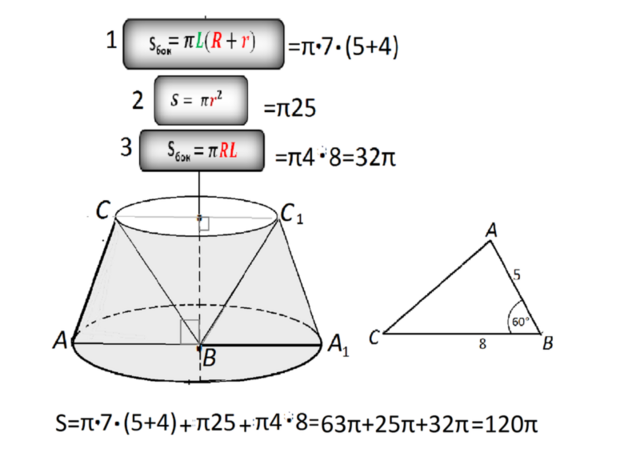
Данная фигура вращения представляет собой усеченный конус, из которого "вырезали" другой конус.
Ясно, что площадь фигуры вращения составлена из:
1)боковой поверхности усеченного конуса с радиусом основания, равным 5 см - меньшей стороне данного треугольника - и образующей, противолежащей углу 60°.
2) площади основания - круга с радиусом 5 см- меньшей стороны треугольника
3) площади боковой поверхности "вырезанного" конуса с образующей СВ=8 см и радиусом основания, противолежащим углу, дополняющему данный угол до 90°
Этот угол равен 90°-60°=30°, и радиус основания "вырезанного" конуса, как противолежащий этому углу, равен половине ВС=8:2=4 см
АС- образующая усеченного конуса.
По т. косинусов
АС²=ВС²+АВ²-2АВ*СВ*cos(60°)
АС²=64+25-2*5*8*1/2АС²=89-40=49
АС=7
------
1) S бок усеч=πL(R+r)
2) S осн=πr²
3) S бок=πrL
Вычисления даны во вложении. Но они очень простые, по приведенным формулам их можно сделать самостоятельно за минуту
.---------
[email protected]