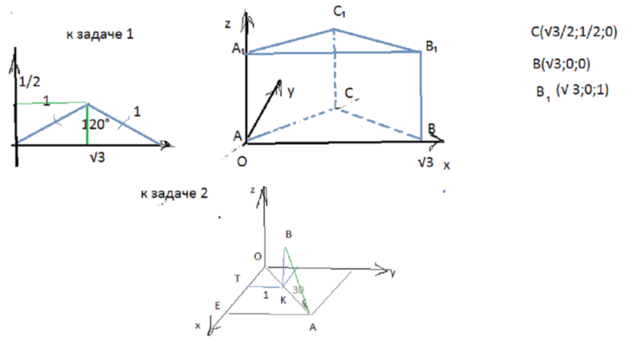
1) cм рисунки в приложении
Расположим призму так, чтобы сторона АВ совпадала с осью ох, А с началом координат.Тогда координаты точек легко найти.
Считаем АС=ВС=1 и АА₁=ВВ₁=СС₁=1
Из треугольника АСВ по теореме косинусов АВ=АС²+ВС²-2АС·ВС·сos 120°=1+1-2·(-1/2)=3
АВ=√3, значит координаты точки
В(√3;0;0)
Проведем высоту из точки С к стороне АВ. Высота равна 1/2- катет против угла в 30°
Значит координаты точки
С(√3/2; 1/2;0)
координаты точки
С₁(√3/2; 1/2;1)
Вектор АВ имеет координаты (√3;0;0), длина вектора АВ=√3
Вектор С₁B имеет координаты (√3- √3/2; 0-1/2;0-1)= (√3/2; -1/2;-1)
Длина вектора С₁B=√(√3/2)²+(-1/2)²+(-1)³=√(3/4)+(1/4)+1=√2


2)ОК=√2, так как кордината точки К(1;1)
ВК=1 ( третья координата точки В равна 1)
У точки А координаты х и у равны, значит она лежит на биссектрисе первого координатного угла , на продолжении ОК.
Из прямоугольного треугольника АВК:
гипотенуза АВ в два раза больше катета ВК, так как катет ВК против угла в 30°
По теореме Пифагора КА²=АВ²-ВК²=2²-1²=3
КА=√3
ТРеугольники ОКТ и ОАЕ подобны. Из подобия
КТ:ЕА=ОК:ОА
1:ЕА=√2:(√2+√3)
ЕА√2=(√2+√3)

Координата точки А по оси оу равна ЕА, но так как и по оси ох такая же координата
ответ

3) Пусть координаты точки M(x;y;z)
Радиус-вектор ОМ имеет такие же координаты.

По условию скалярное произведение равно 0
7х+0у+0z=0
Значит х=0

По условию скалярное произведение равно 0
0х+0у+3z=0
значит z=0
у- любое
Множество точек пространства, у которых первая координа 0, вторая - любая, третья 0 - ось оу