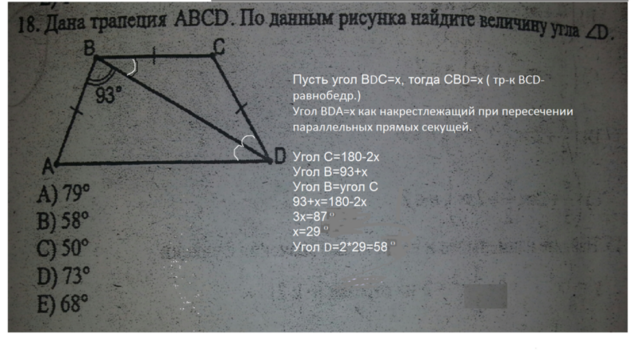
Дана трапеция АВСD. По данным рисунка найдите величину угла D.
Рассмотри рисунок.
Ясно. что т
рапеция АВСD равнобедренная . Угол АВD=93°, а меньшее основание равно боковым сторонам.
Следовательно, диагональ ВD- основание равнобедренного треугольника ВСD, и углы
СВD и СDВ равны.
Угол ВDА как накрестлежащий при пересечении параллельных прямых секущей равен углу СВD.
Т.к. трапеция равнобедренная, в ней углы при основаниях равны.
Угол А=углу D
Угол В=углу С
Пусть угол ВDС=х
Тогда СDА=2х=ВАD
Сумма углов, прилежащих одной боковой стороне трапеции, равна 180°
Угол В+угол А=2х+93+х=180
3х=87
х=29
Угол D=29°*2=
58°