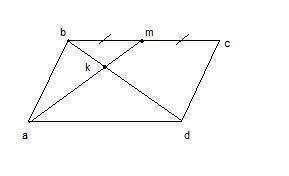
Рассмотрим треугольники bkm и dka. Они подобны по первому признаку: два угла одного треуг-ка соответственно равны двум углам другого:
- углы bkm и dka равны как вертикальные;
- углы bmk и dak равны как накрест лежащие углы при пересечении двух параллельных прямых ad и bc секущей am.
Для подобных треугольников можно записать отношение сходственных сторон:
bm : da = 1 : 2, k=1/2 (поскольку точка m - середина стороны bc по условию, и ad=bc как противоположные стороны параллелограмма).
Значит и bk : dk = 1 : 2.
bd=bk+dk=1 часть + 2 части = 3 части.
Таким образом bk : bd = 1 : 3