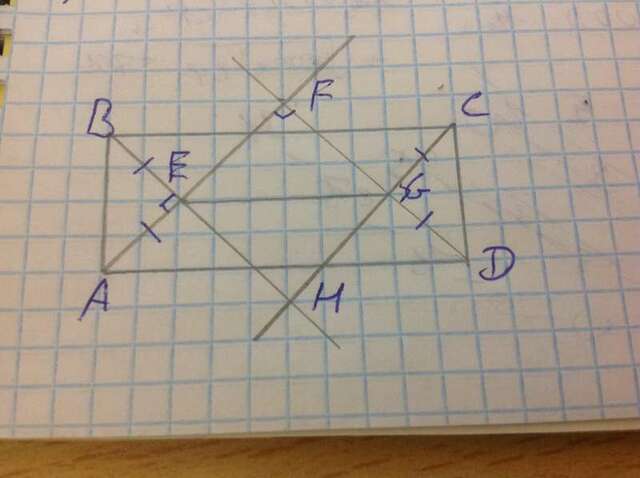
Пусть в прямоугольнике ABCD биссектрисы пересекаются в точках E,F,G,H. Докажем, что EFGH - квадрат. В треугольнике AFD углы A и D равны 45 градусам, тогда угол F равен 90 градусам. Аналогично, в треугольнике BCH углы B и C равны 45 градусам, а угол H равен 90 градусам. В треугольнике ABE углы A и B равны 45 градусам, тогда угол E равен 90 градусам. Тогда и угол FEH равен 90 градусам (вертикальные углы равны). Аналогично, в треугольнике CDG углы C и D равны 45 градусам, тогда угол G равен 90 градусам и угол FGH равен 90 градусам. Таким образом, все углы четырехугольника EFGH равны 90 градусам и этот четырехугольник является прямоугольником.
Теперь докажем, что соседние стороны EF и FG этого прямоугольника равны. Треугольники ABE и CDG равны, так как каждый из них - равнобедренный и прямоугольный и их гипотенузы равны. Тогда AE=DG. Треугольник ADF является равнобедренным и прямоугольным, тогда AF=DF. Тогда EF=AF-AE, GF=DF-DG, откуда EF=GF, треугольник EFG равнобедренный и EF=FG. Так как в прямоугольнике EFGH соседние стороны равны, этот прямоугольник - квадрат, что и требовалось доказать.