Нужно решение второй части задачи, радиус я нашла, как расстояния найти?Около...

Question

Нужно решение второй части задачи, радиус я нашла, как расстояния найти?
Около равнобедренного треугольника АВС (АВ = ВС) с основанием АС = 6 и боковой стороной АВ = 5 описана окружность. Найдите радиус окружности и расстояния от вершин А и В до касательной, проведенной через точку С

Answer 1

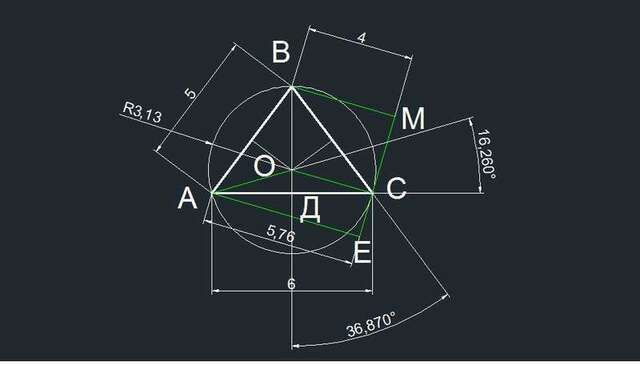
Высота ВД треугольника АВС равна √(5²-(6/2)²) = √(25-9) = 4.
Угол ДВС обозначим α.
sin α = 3/5,   cos α = 4/5.
Касательная ЕМ к окружности в точке С перпендикулярна радиусу ОС, а, значит, расстояния от точек А и В до этой касательной перпендикулярны ей и параллельны ОС.
Угол СВМ равен углу ДВС и ОСВ. Тогда ВМ = 5*cos α = 5*4/5 = 5. ОВ и ОС - радиусы, значит, угол ОВС = ОСВ.
Угол АСЕ = 90-Отсюда расстояние АЕ =6*sin 2α = 6*2*sin α*cos α =
= 6*2*(3/5)*(4/5) = 144/25 = 5,76.

---