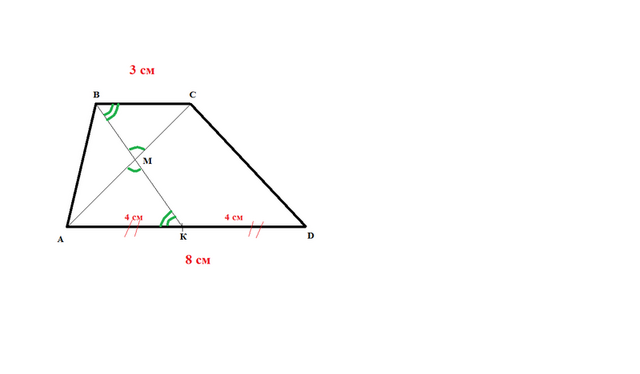
1) В трапеции ABCD с основаниями AD=8 см, BC=3 см, точка К - середина AD.
Диагональ AC (здесь была опечатка FC) пересекается с BK в точке М. Найти отношение BM к MK.
РЕШЕНИЕ
сделаем построение по условию
AC -диагональ
треугольники BMC ~ AMK - подобные по двум углам (признак подобия)
< BMC , < AMK -вертикальные (равны)
< СBM , < AКM -скрещивающиеся (равны)
АК = AD/2=8/2 = 4см
коэффициент подобия треугольников k=BC: AK= 3:4
соответствующие стороны треугольников имеют такое же отношение
BM :MK = BC: AK= 3:4
ОТВЕТ BM :MK = 3:4
2) В параллелограмме ABCD биссектриса острого угла BAD пересекает ВС в точке К,
а продолжение CD - в точке F, CF относится к FD как 2 к 5.
Найти стороны параллелограмма, если его периметр равен 64 см.
РЕШЕНИЕ
сделаем построение по условию
< BAK =
< BAK =
CF : FD = 2 : 5 - по условию, тогда CF : СD = 2 : 3 - из первого отношения
треугольник АВК - равнобедренный < BAK = <ВКА -углы при основании</p>
Пусть АВ=х , тогда ВК=х
треугольники FKC ~ ABK - подобные по двум углам (признак подобия)
коэффициент подобия треугольников k= CF : AB =CF : CD = 2 : 3
тогда СК : ВК = CF : AB = 2 : 3 <----но BK=x</p>
тогда СК : х = 2 : 3 ; CK =2x/3
тогда BC =BK + CK = x + 2x/3 = 5x/3
имеем две стороны в параллелограмме
AB=x ; BC =5x/3
формула периметра P= 2* (AB+BC) = 2* (x +5x/3)=2*8x/3 =16x/3
по условию P=64 см , тогда 64 =16x/3 ;
x = 12 см - одна сторона
5x/3 = 5*12 /3 = 20 см -вторая сторона
ОТВЕТ 12 см ; 20 см