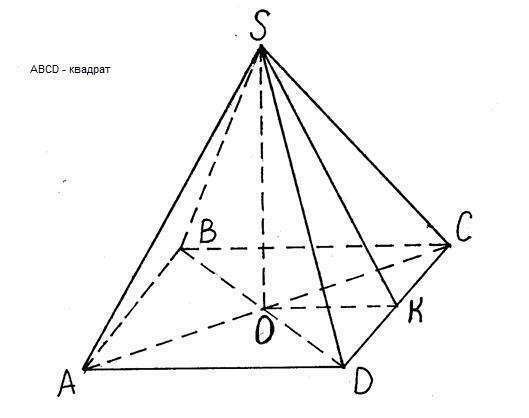
В правильной четырехугольной пирамиде SABCD в основании - квадрат ABCD, а вершина S проецируется в центр основания O. Значит ОК=ВС/2=4/2=2.
Рассмотрим прямоугольный треугольник SOK:
SK=OK/cos α=2/cos α
Теперь найдем площадь боковой грани (треугольника DSC).Т.к. он равнобедренный (боковые рёбра правильной пирамиды равны) , то площадь
Sгр=SK*CD/2=2/cos α*4/2=4/cos α
Площадь боковой поверхности правильной пирамиды равна площади всех ее боковых граней:
Sбок=4Sгр=4*4/сos α=16/cos α
Площадь основания Sосн=4*4=16
Площадь полной поверхности правильной пирамиды равна
Sп=Sбок+Sосн=16/ cos α+16=16(1/cos α+1)