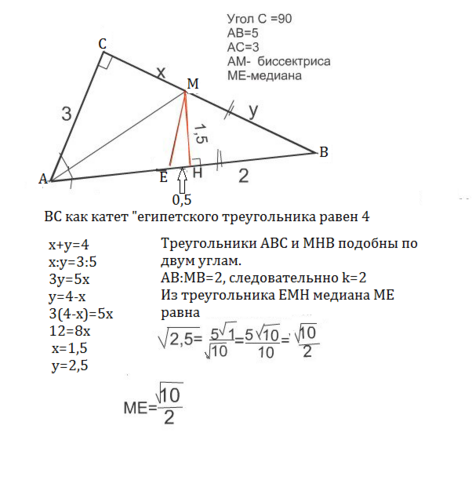
Сделаем рисунок.
Треугольник АВС- так называемый "египетский, с отношением сторон 3:4:5 и второй катет ВС = 4
Проведем в нем биссектрису АМ.
Обозначим отрезки, на которые поделена СВ, как х и у.
Так как СВ=4, х+у=4
у=4-х
Применим свойство биссектрисы треугольника, а именно:
Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам:
х:у=3:5, следовательно,
3у=5х. Подставим в это уравнение значение у, найденное из первого уравнения и
решим его.
Получим:
х=1,5 , у=2,5
Проведем из М к ВЕ высоту МН.Δ АВС и ΔМВЕ подобны. В них равны
углы, а коэффициент подобия равен АВ:МВ=2
Отсюда ВН=2,МН=1,5
Так как ВЕ=2,5 ( точка Е делит медианой сторону АВ на 2 равные части по 2,5), ЕН=0,5
Из треугольника ЕМН находим ЕМ=√2,5. Путем несложных преобразований
переведем √2,5 в (√10):2
Во втором приложении дан вариант решение это задачи.