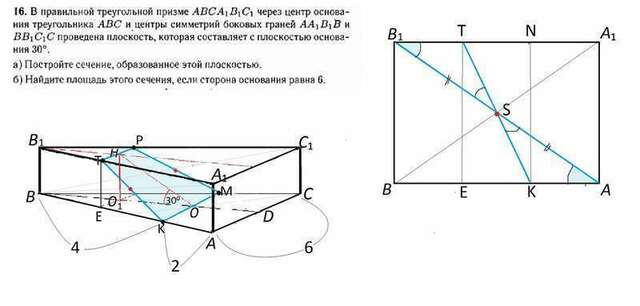
В правильной треугольной призме АВСАВС через центр основания треугольника АВС и центры симметрии боковых граней АА₁В₁В и ВВ₁С₁С проведена плоскость, которая составляет с плокостью основания 30°
а)Постройте сечение, образованное этой плоскостью.
б) Найдите площадь этого сечения, если сторона основания равна 6.
Центр О основания этой призмы - это центр вписанной в основание окружности.
Центры симметрии боковых граней - точки пересечения их диагоналей ( на рисунке они отмечены красными точками).
Призма правильная, грани призмы равны между собой.
Проведем через центр основания прямую КМ, параллельную АС. Это линия пересечения плоскости сечения и плоскости основания.
Через точки К и М и через центры симметрии боковых граней проведем прямые до пересечения с ребрами верхнего основания в точках Т и Р.
Соединив точки. Т, Р, М и К, получим сечение КТРМ, которое является трапецией.
Точка пересечения О медиан треугольника по свойству медиан делит их в отношении 2:1, считая от вершины.
ВО: ОD=2:1
ВD=АВ*sin (60°)=6√3):2=3√3 ⇒
ВО=2√3
ОD=√3
КМ отсекает от треугольника АВС подобный ему МВК с отношением ВК:КА= 2:1, считая от В.
АК=6:3=2, ВЕ=6:3*2=4
Рассмотрим отдельно рисунок грани АВВ1А1
Найдем ее центр симметрии - точку пересечения диагоналей S.
Проведем через S из К прямую до пересечения с В₁А₁
в точке Т.
По свойству диагоналей прямоугольника В₁
S=SA.
В₁А - секущая при параллельных А₁В₁
и АВ.
Углы ТВ₁А=В₁
АК как накрестлежащие.
Углы при S равны как вертикальные.
△ В₁SТ=△KSA⇒ ТВ₁
=КА.
Так как ВК=2КА, В₁Т=АК=ВE , из подобия треугольников МВК и МВ₁Р отрезок ОО₁
на высоте ВD основания равен половине ВО.
ВО=2√3
OO₁
=√3
В₁Н=ВО₁
НО₁ || ВВ₁ и перпендикулярна ОО₁
Из треугольника ОНО₁
найдем высоту трапеции НО:
НО=ОО₁
:sin (30°)=√3):{(√3):2}=2
Треугольник ВКМ равносторонний, стороны его равны 4 см
ТР равна средней линии треугольника МАВ и равна половине КМ.
ТР=2.
Площадь трапеции равна половине произиведения ее высоты на полусумму оснований.
S МКТР=НО*(ТР+КМ):2=2*(2+4):2=6 единиц площади