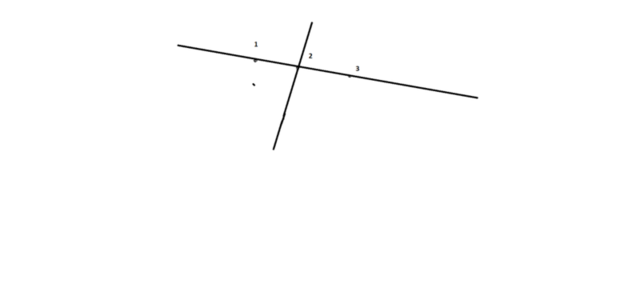
5) На основе первой аксиомы стереометрии: через любые 3 точки
можно провести плоскость и притом только одну. А как быть для точек лежащих на одной прямой. Проведем через точку 2 произвольную прямую а в пространcтве. Тогда из аксиомы 3: Если две разные прямые имеют общую точку, то через них можно провести плоскость, и притом единственную.
Тогда выходит что эта плоскость проходит через прямую на которой лежат эти точки. То есть эти точки лежат на данной плоскости. ЧТД
Понятно ,что можно провести бесконечное множество прямых в пространстве через заданную точку 2 . А значит через эту прямую можно провести бесчисленное множество плоскостей. То и через 3 данные точки соответственно.
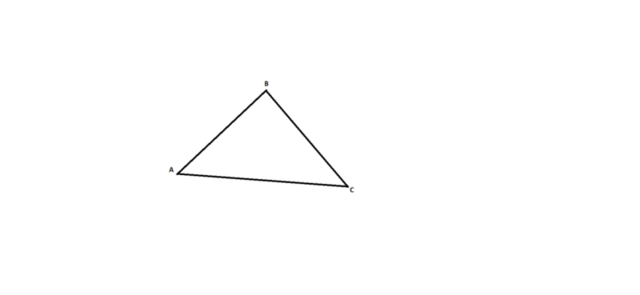
6) Ясно что прямые AB и BC пересекаются тк они имеют общую точку A . То из аксиомы 3 они лежат в одной плоскости и только в одной . Анологично пересекаются и прямые BC и AC,в общей точке C,то прямые BC и AC тоже лежат в одной плоскости. Но эти две пары прямых не могут лежать на разных плоскостях. ТК в каждой из пар есть обшие точки A,B,C. А любые 3 точки пространства лежат только в одной плоскости. (1 аксиома) Таким образом все 3 прямые лежат в одной плоскости.