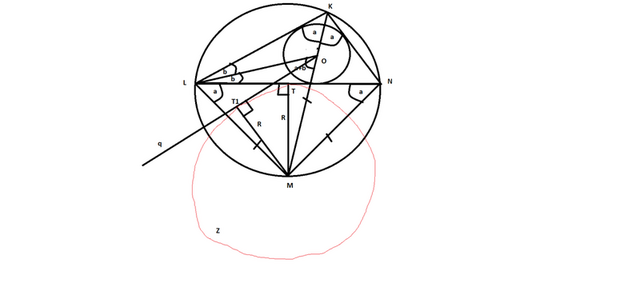
Да очень красивое задание.
Треугольник MLN-равнобедренный,откуда ΔMLN=ΔMNL.
Поскольку 4 угольник KLMN-вписан в окружность,то углы опирающиеся на равные дуги равны: ΔMLN=ΔMKN=ΔMNL=ΔMKL=a. Откуда KM-биссектриса ΔLKN.
И наконец самое главное: раз центр вписанной окружности лежит на точке пересечения его биссектрис,то очевидно , что центр вписанной в треугольник KLN окружности лежит на биссектрисе KM. (Значит KM проходит через центр вписанной окружности).
И вот мы подобрались к истинному чуду этой задачи: проведем через центр вторую биссектрису LO. (Центр лежит и на биссектрисе ΔNLK соответственно).
Обозначим разбитые ей углы по b. Из суммы углов треугольника верно что :ΔLOK=180-(a+b) ,также ΔLOK смежный угол с ΔLOM.
Значит : ΔLOM=180-(180-(a+b))=a+b,но вот еще одна неожиданность:
ΔMLO=ΔMLN+ΔNLO=a+b. Опа ΔMLO=ΔLOM, то треугольник MLO-равнобедренный. ML=MO.
И вот второе чудо этой задачи:
Проведем перпендикуляр MT на LN и перпендикуляр MT1 на прямую q ||LK. ΔT1OM=ΔLKM=a ,как соответственные углы при параллельных
прямых q и LK. (Там не подписал угол a ,но суть ясна надеюсь).
И вот оно: треугольники MT1O и MTL равны по стороне и двум прилежащим к ней углам. Действительно: ΔT1OM=ΔMLT=a.
Поскольку у этих двух треугольников есть по равному прямому углу. То из соображений суммы углов треугольника: ΔT1MO=ΔLMT и равны стороны : ML=MO ,откуда следует вышесказанное утверждение.
Тогда: MT=MT1,то есть если окружности Z касается прямой LN соответственно в точке T (Тк радиус перпендикулярен касательной). То выходит что MT=MT1=R.
А значит радиус окружности Z перпендикулярен прямой q . И T1 принадлежит окружности Z. То есть q-касательная к окружности Z :)
ЧТД.