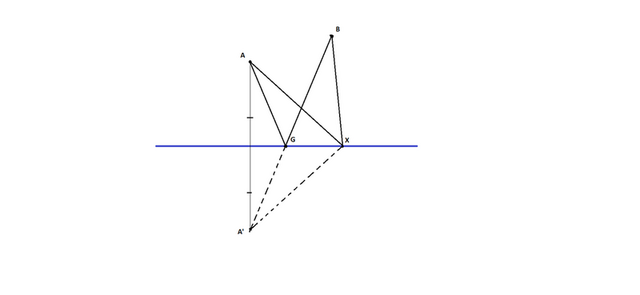
Отразим точку A относительно линии реки. A' -отражение точки A. Соединим точки A' и B . И в пересечении с линией реки обозначим точку G. Как вы наверное догадались, это и есть та золотая точка ,что сумма расстояний от нее до пунктов наименьшая. Причем A'G отражение отрезка AG. A'G=AG.Откуда : AG+BG=A'G+BG=A'B.
Докажем это:
Отметим на линии реки произвольную точку X.
Откуда по тому же принципу : AX отражение A'X. AX=A'X.
Таким образом: AX+BX=A'X+BX
По неравенству треугольника A'XB:
A'X+BX>=A'B
То есть: AX+BX>=A'B
А значит расстояние A'B является наименьшим из всех сумм расстояний при произвольно взятых X.
При этом треугольник A'XB вырожденный.
Что возможно лишь когда точка X совпадает с точкой G.
Таким образом точка G искомая.