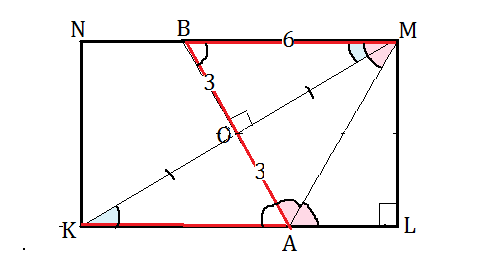
Через середину диагонали KM прямоугольника KLMN перпендикулярно этой диагонали проведена прямая, кторая пересекает стороны KL и MN в точках A и В соответственно. Известно, что AB=BM=6 см. Найдите большую сторону прямоугольника.
Так как точка О - середина диагонали КМ, отрезки КО и ОМ равны.
Рассмотрим прямоугольные треугольники АОК и ВОМ. Они имеют равные катеты КО=ОМ по условию и равные острые углы АКО и ВМО - накрестлежащие при параллельных прямых и секущей КМ. ⇒
Эти треугольники равны. ⇒
ВМ=АК=6 см, ВО=АО=3 см, ⇒
МО - медиана треугольника АВМ.
Так как МО⊥ВА по условию, она является и высотой треугольника ВМА. Треугольник, в котором медиана является высотой - равнобедренный. ВМ=АМ. Но по условию и АВ=ВМ, следовательно,
треугольник АВМ - равносторонний, все его стороны равны 6 см. Рассмотрим прямоугольные треугольники ALM и AOM.
Они имеют общую гипотенузу АМ и равные острые углы ОАМ и МАL, т.к. углы ВАМ и ВМА равны как углы правильного треугольника, а углы ВМА и МАL равны, как накрестлежащие.
Следовательно, ∆ МОА=∆ МАL, и АL=3см
Большая сторона прямоугольника равна КА+AL=6+3=9 см