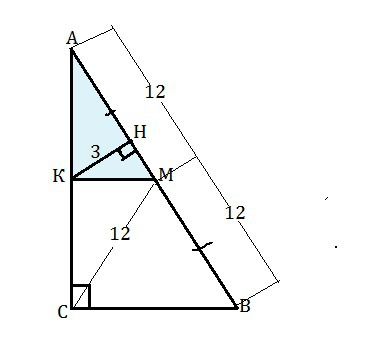
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине. ⇒ АВ=12•2=24 см
Пусть середина АС - точка К. Тогда КМ соединяет середины двух сторон. КМ- средняя линия ∆ АВС.
Средняя линия треугольника параллельна третьей стороне и делит его на подобные треугольники.
КМ -параллельна ВС, угол АКМ=90º, ∆ АКМ - прямоугольный.
Расстояние от К ( середины АС) до гипотенузы - перпендикуляр КН, высота ∆ АКМ.
∆ АКМ
~∆АВС с коэффициентом подобия АМ:АВ= k=1/2
Площади подобных фигур относятся как квадрат их коэффициента подобия.
S∆ AKM:S∆ ABC=
k²=
1/4
S∆ ABC=4 S∆
AKM
Площадь ∆ АКМ=КН•AN
:2=3•12
:2=18 см²
S∆ ABC=18•4=72см²