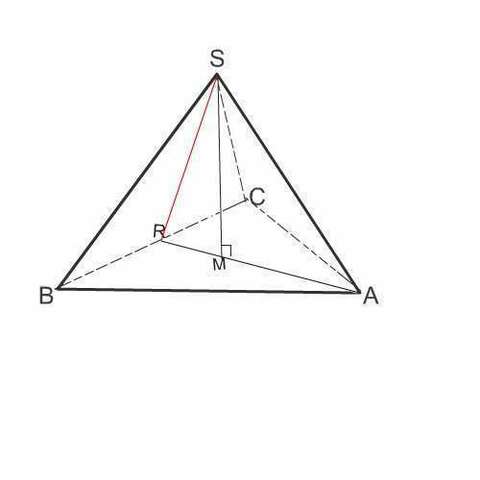
Правильной треугольной пирамидой называется пирамида, основание которой - равносторонний треугольник, а грани - равные равнобедренные треугольники.
Задача решена исходя из того, что точка М - основание высоты SM пирамиды.
Для решения задачи нужно знать апофему SR, так как площадь боковой поверхности состоит из суммы площадей боковых граней.
Площадь же боковой грани равна площади треугольника с высотой, равной апофеме и основанием, равным основанию равностороннего треугольника АВС.
Апофему SR найдем по теореме Пифагора:
SR²=RM²+SM²
RM нам неизвестна, ее мы найдем по формуле высоты равностороннего треугольника, выраженной через его сторону.
h=(а√3):2.
RM равна трети этой высоты треугольника ( которая в то же время и медиана равностороннего треугольника и потому точкой пересечения медиан делится в отношении 2:1, считая от вершины. Высота правильной пирамиды опирается на эту точку.)
h=(4√3):2=2√3
RM=(2√3):3
Находим
SR²=12:9+9= 93/9
SR=(√93):3
Sбок=3∙{ 2∙(√93):3}= 2√93 см²